问题1：不同充盈体积下，球囊个体的充盈直径在测试时因充盈量，膨胀程度等有差异？
分析：以下说明以TPU材料为例：
TPU（热塑性聚氨酯）的应力-应变曲线通常呈现出以下几个阶段：
（1）初始阶段：在初始充载过程中，应力与应变之间呈现线性关系。这是因为TPU材料在低应力范围内表现出弹性行为，即应力随着应变的增加而现行增加。
（2）弹性阶段：当应力增加到一定程度时，TPU材料进入弹性变形阶段。在该阶段，应力-应变曲线仍保持线性关系，但在卸载后可以完全恢复原状，没有塑性形变。
（3）屈服阶段：当应力继续增加，TPU材料会达到其屈服点，即开始发生可逆的塑性变形。在该阶段，随着应变的增加，应力-应变曲线呈现出更陡峭的曲线，材料在该阶段经历一定程度的塑性形变。
（4）稳定塑性阶段：在超过屈服点后，材料进入稳定塑性阶段。在该阶段，材料逐渐失去弹性恢复能力，发生的塑性形变不再完全恢复。应力-应变曲线变得平缓，表示材料的变形速率逐渐减小。
（5）断裂阶段：当应力继续增加，直至达到TPU的断裂应力时，材料断裂。此时，应力-应变曲线急剧下降，表示材料无法承受更大的应力发生断裂。
以上是从拉伸的角度来讲，充盈也相当于一种拉伸。在弹性阶段以前，应变和应力是呈线性的关系，应变应随应力的增加而线性增加。但是我们的囊体的变化是以球体的形态在变化，球的体积V=4/3πr3，半径r和体积并不是线性的关系，是3次幂的关系，所以充同样的体积的水，半径不是线性变化的。
在弹性形变后，因为分子链的运动、断裂等其他因素的存在，不再是线性关系，直径与体积的对比就没有明显的关系式了，要根据实际情况分析。
问题2：关于球囊破裂模式，是否无法固定？比如轴向和径向破裂，混合形式的破裂都可能发生？原理如何解释？
分析：
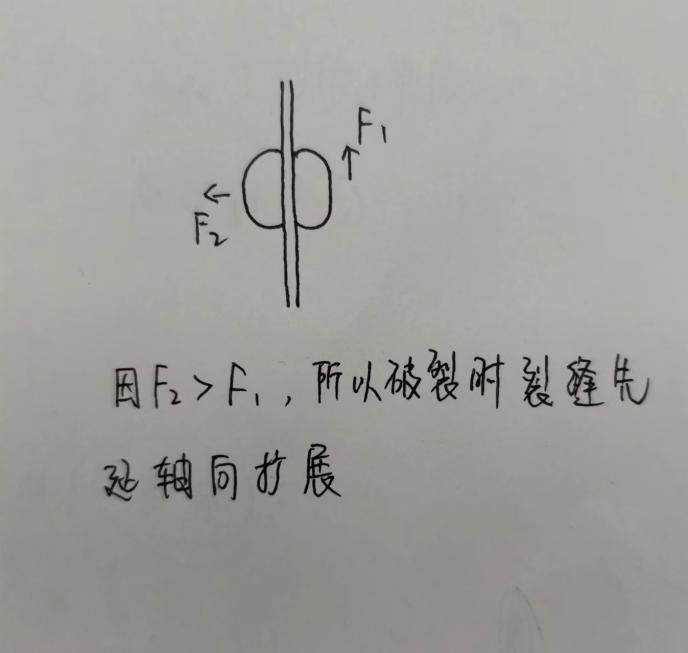
如图，球囊在扩张状态下（非极限爆破），横向的力F2＞轴向力F1，因此球囊在破裂时会轴向撕裂。待裂纹扩展到两端时，由于力的方向发生了改变，横向力稍大于轴向力时，裂纹会向横向方向扩展一点，就形成了如下的破裂方式（天然乳胶、TPE、硅胶的球囊也是同样的破裂方式）。
下一条： 医用天然乳胶球囊的概述和应用方向介绍
